Rethinking the Augmentation Module in Contrastive Learning: Learning Hierarchical Augmentation Invariance with Expanded Views
CVPR 2022 paper.
TLDR
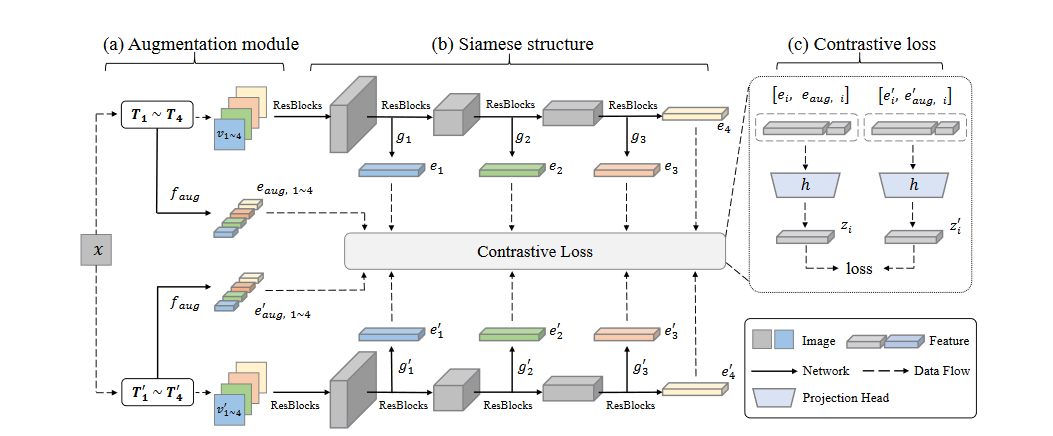
1.Iteratively apply different augmentation methods
2.Extract losses from multiple stages of backbone network
3.Embed information about augmentation, in addition to original image feature.
Quick Look
- Authors & Affiliation: Junbo Zhang
- Link: https://openaccess.thecvf.com/content/CVPR2022/papers/Zhang_Rethinking_the_Augmentation_Module_in_Contrastive_Learning_Learning_Hierarchical_Augmentation_CVPR_2022_paper.pdf
- Comments: CVPR 2022
- Relevance: 3
Research Topic
- Category (General): Contrastive Learning
- Category (Specific): Contrastive Learning
Paper Summary (What)
- Problem statement
- First, the artificial choice of augmentation types brings specific representational invariances to the model.
- i.e. each different augmentation methods have different amount of impact, but monotonically regarded as same.
- Second, the strong data augmentations used in classic contrastive learning methods may bring too much invariance in some cases
- i.e. when applying too much color augmentation to red roses will extend invariances to non-realistic cases, like green roses.
- Solutions
- Iteratively apply different augmentation methods
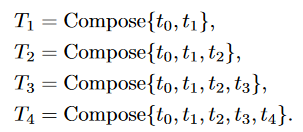
Conventional contrastive learning methods apply one or more augmentations separately. Instead, incrementally apply different augmentations to maximize pairs.
- Extract contrastive loss from multiple stages.
Conventional contrastive learning methods acquire contrastive loss at the end of the network, based on the pair of outputs.
Instead, check contrastive loss for even phases before output.
For example, check contrastive loss for layer \(1,2, \cdots l\)
- Embed augmentation information into input.
Given \(L_{contrastive}(z_a, z_b)\),
Normal contrastive learnings:
\(z = f(\text{feature})\)
Suggested method:
\(z = f(\text{feature}, \text{augmentation embedding})\),
when \(\text{augmentation embedding} = g(\text{color information}, \text{rotational angle}, \text{masking box location and size}, \cdots )\)
Notable References
Thoughts
Stacking augmentation methods may have dependency issues.
–> e.g. color jittering and gray scale transform both affect color feature embedding.
–> Finding (independent) augmentation basis operations may be a solution. i.e. independent basis operations does not affect each other
–> Making a superset of basis operations makes the maximum set of possible augmentation pairs!
CAM is not regarded as a criterion.
–> Not only about the classification result, but also the feature itself should be compared in pairs.
–> i.e. feature itself could be an input for \(L_{contrastive}\)
–> Relevent metric would be (grad) CAM.
Footnote
아래와 같은 양식을 활용한다.
#
## Quick Look
- **Authors & Affiliation**: [Authors][Affiliations]
- **Link**: [Paper link]
- **Comments**: [e.g. Published at X / arXiv paper / in review.]
- **TLDR**: [One or at most two line summary]
- **Relevance**: [Score between 1 and 5, stating how relevant this paper is to your work. Usually filled in at the end.]
# Research Topic
- **Category** (General):
- **Category** (Specific):
# Paper Summary (What)
[Summary of the paper - a few sentences with bullet points. What did they do?]