Seminars
학교에서는 종종 AI 세미나가 열리고, 그 중에는 AI 대학원 에서 진행하는 세미나 수업으로 인해 열리는 경우가 대부분이다.
그냥 흘려 보내기에는 아까우니까 정리를 하면 좋겠다는 생각이 들었다.
Seminar Info
- Speaker : UNIST MTH 김정은 교수님
- Topic : Neurocomputation - Hodgkin and Huxley Model
Memos
- Computational Neuroscience : Neuron을 수학적으로 모델링
- spatial scale : 엄청 다양. 전체 뇌는 $10^{12}$ 개 neurons, 전두엽/측두엽 , … , 분자 단계
- temporal scale : years 장기기억, ms reaction time, nano sec ion channels.
- Objective : 신경 세포를 어떻게 수리적으로 modeling 할 것인가?
- analytical models:
- non-linear DE, linear stability analysis
- graph theory
- probability, stochastic DE
- activation threshold : 의미 있는 정보/신호 만 전달!
- Hodgkin-Huxley Model:
- neuron을 RC circuit 으로 modeling,
- 미분 방정식 형태로 기술.
- 기본적으로 Kirchihoff 법칙 적용. $ I = \sum I_x $
$\rightarrow$ EE/CSE의 information 으로 바꿔서 적용 가능? Information bottleneck?
- simple model:
- $\frac{dm}{dt} = \alpha_m (1-m) - \beta_m m$
- steady state, DE equilibrium solution.
- 4 variable -> 2 variable 줄일 수 있음!
- eg. $\alpha n(t) + \beta h(t) = const$ 형태로 근사,
- 변수의 종류/개수를 줄임.
- integrate-and-fine model : low computational complexity.
- Memory formation 과도 연결됨.
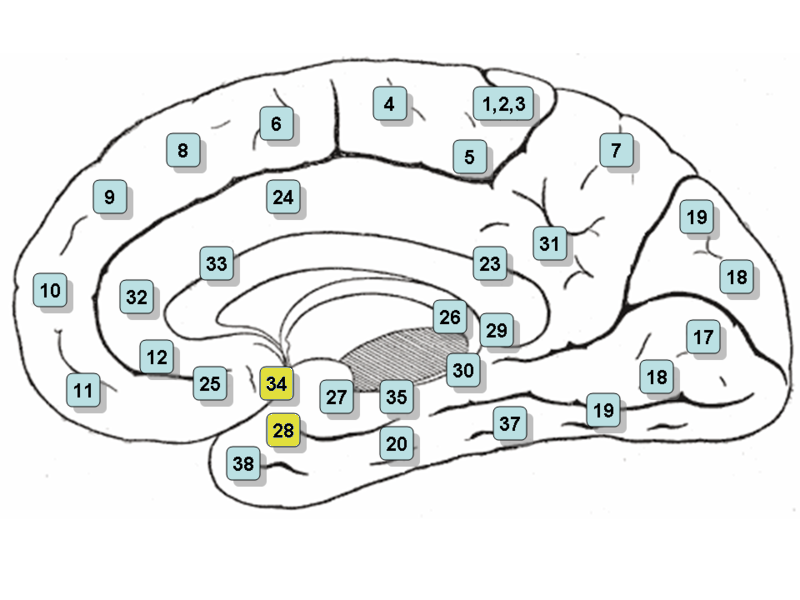
- Entorhinal cortex : pyramidal neuron model 과 연결?
- mixed mode oscillation : 외부 신호 없어도 계속 resting 에 있는게 아니라, burst 있음.
- graded-persistent activity: 정보를 저축하는 특징.
- Prof.김정은’s work:
- 깨어있는 상태 촉진 물질과 자고 있는 상태 촉진 물질 상호 피드백 작용.
- 시간에 따라 양 측정 $\rightarrow$ prob.distribution 구할 수 있음.
- 이를 확률 미분 방정식으로 모델링
- 다만 풀 때 마다 다름. probability 정해져 있지만, event 결과 다름.
- TL;DR : math + neuro science, develop and analyze math.models for neuron activity and pattern.
Images
Conclusion
- 제목을 보고 AIGS에서 잘못 알고 왔을 수 있다는 말에 뜨끔했다.
- 하지만 inspring.